
English Version | Leitseite des Instituts
Die Forschungsschwerpunkte des Instituts liegen im Bereich der Diskreten Mathematik und ihrer Anwendungen, insbesondere zu nennen sind Kombinatorische Optimierung und Chip-Design.

|
Die Kombinatorische Optimierung hat in den letzten Jahrzehnten wegen ihrer immensen Anwendungsrelevanz zunehmend an Bedeutung gewonnen. Am Forschungsinstitut für Diskrete Mathematik spielt sie schon immer eine wesentliche Rolle. Ausdruck dessen sind zahlreiche wegweisende Arbeiten der hiesigen Wissenschaftler und Gäste zu den unterschiedlichsten Fragestellungen der Kombinatorischen Optimierung. Der Artikel [1] gibt eine kurze Einführung. Einen umfassenden Überblick gibt das hier entstandene Standardwerk "Combinatorial Optimization" [2], von dem bereits sechs englische Auflagen erschienen sind. Wir richten häufig diverse internationale wissenschaftliche Tagungen aus. |

|
Das Chip-Design ist vielleicht das interessanteste und vielseitigste Anwendungsgebiet der Mathematik überhaupt. Ohne Methoden insbesondere der Diskreten Mathematik kann heute keiner der hochkomplexen Chips mehr entworfen werden. Viele dieser Methoden sind hier am Institut entwickelt worden. Unsere enge Kooperation mit der Industrie ermöglicht das Arbeiten an den aktuellsten Technologien und den komplexesten Chips. Unsere "BonnTools" [3], die unter anderem innovative Algorithmen für Placement, Routing, Timing-Optimierung und Layout auf Transistorebene beinhalten, werden weltweit eingesetzt. Der Artikel [4] gibt eine kurze Einführung in das Chip-Design. Einen umfassenderen Überblick gibt [5]. |
|
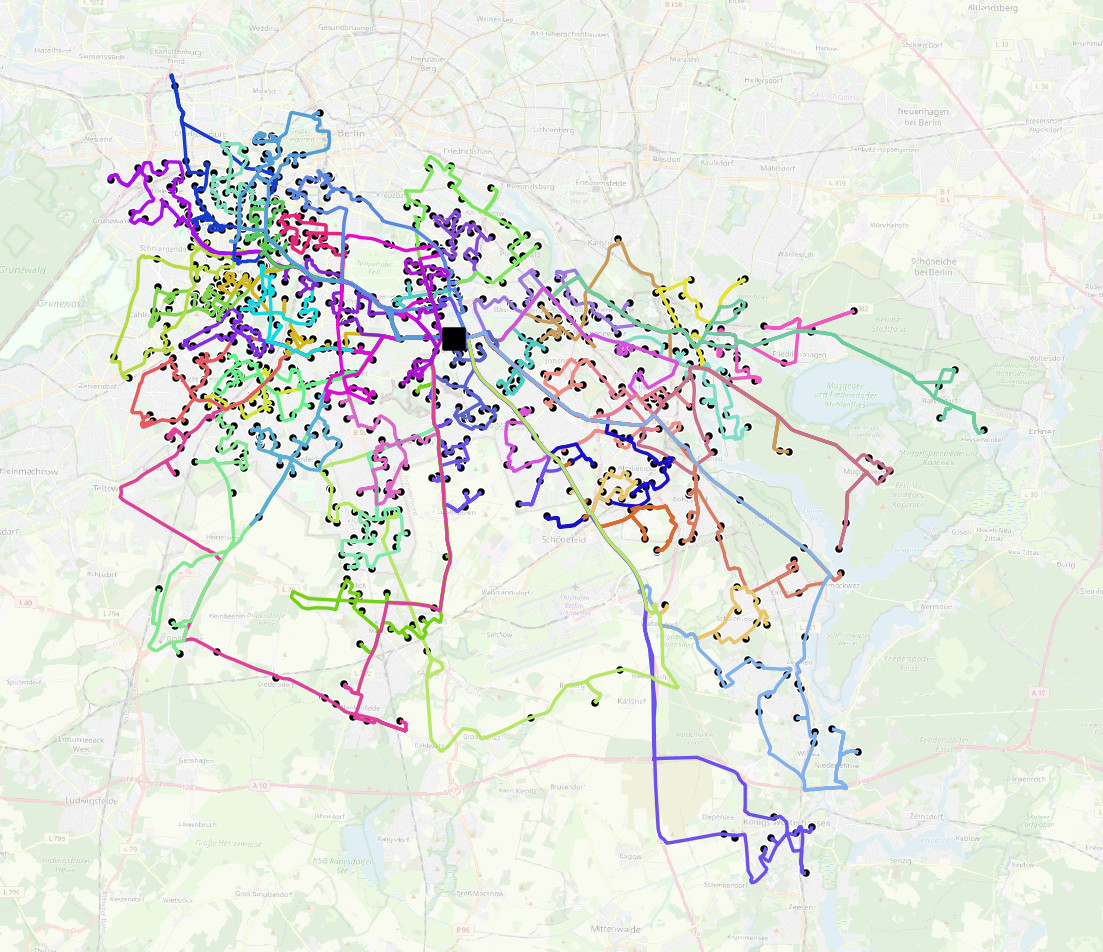
Vehicle Routing ist ein weiteres Anwendungsgebiet, dem wir uns widmen. Basierend auf unseren Forschungsergebnissen zum Rundreiseproblem (TSP) [6] haben wir vor einigen Jahren eine neue Kooperation über die Optimierung von Zustelldiensten begonnen. Neben dem theoretischen Studium von Approximationsalgorithmen für Rundreise- und Vehicle-Routing-Probleme (siehe z.B. [7]) entwickeln wir einen Algorithmus für Tourenplanung in der Praxis, unter Berücksichtigung von tageszeitabhängigen Fahrtzeiten, heterogenen Flotten, Zeitfenstern und vielen anderen Nebenbedingungen (siehe [8]). |
Zu den genannten Hauptthemen kann als einführende Literatur empfohlen werden:
| [1] | J. Vygen: Combinatorial Optimization. Princeton Companion of Applied Mathematics, Princeton University Press 2015 [Download] |
| [2] | B. Korte, J. Vygen: Combinatorial Optimization: Theory and Algorithms. Springer, Berlin, Sixth Edition 2018. [Informationen] |
| [3] | B. Korte, D. Rautenbach, J. Vygen: BonnTools: Mathematical innovation for layout and timing closure of systems on a chip. Proceedings of the IEEE 95 (2007), 555-572 [Download] |
| [4] | S. Held, S. Hougardy, J. Vygen: Chip Design. Princeton Companion of Applied Mathematics, Princeton University Press 2015 [Download] |
| [5] | S. Held, B. Korte, D. Rautenbach, J. Vygen: Combinatorial optimization in VLSI design. In: Combinatorial Optimization: Methods and Applications (V. Chvátal, ed.), IOS Press, Amsterdam 2011, pp. 33-96 [Download] |
| [6] | V. Traub J. Vygen: Approximation algorithms for traveling salesman problems. Cambridge University Press 2025 (im Druck) |
| [7] | J. Blauth, V. Traub, J. Vygen: Improving the approximation ratio for capacitated vehicle routing. Mathematical Programming 197 (2023), 451-497 [arXiv] |
| [8] | J. Blauth, S. Held, D. Müller, N. Schlomberg, V. Traub, T. Tröbst, J. Vygen: Vehicle routing with time-dependent travel times: theory, practice, and benchmarks. Discrete Optimization 53 (2024), 100848 [arXiv] |
Das Forschungsinstitut für Diskrete Mathematik unterhält zahlreiche internationale Kooperationen und Drittmittelprojekte. Besonders erwähnenswert sind: